https://codeforces.com/contest/1921/problem/E
Problem - E - Codeforces
codeforces.com
문제
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output
Alice and Bob are playing a game on a checkered board. The board has ℎℎ rows, numbered from top to bottom, and 𝑤 columns, numbered from left to right. Both players have a chip each. Initially, Alice's chip is located at the cell with coordinates (𝑥𝑎,𝑦𝑎) (row 𝑥𝑎, column 𝑦𝑎), and Bob's chip is located at (𝑥𝑏,𝑦𝑏). It is guaranteed that the initial positions of the chips do not coincide. Players take turns making moves, with Alice starting.
On her turn, Alice can move her chip one cell down or one cell down-right or down-left (diagonally). Bob, on the other hand, moves his chip one cell up, up-right, or up-left. It is not allowed to make moves that go beyond the board boundaries.
More formally, if at the beginning of Alice's turn she is in the cell with coordinates (𝑥𝑎,𝑦𝑎), then she can move her chip to one of the cells (𝑥𝑎+1,𝑦𝑎), (𝑥𝑎+1,𝑦𝑎−1), or (𝑥𝑎+1,𝑦𝑎+1). Bob, on his turn, from the cell (𝑥𝑏,𝑦𝑏) can move to (𝑥𝑏−1,𝑦𝑏), (𝑥𝑏−1,𝑦𝑏−1), or (𝑥𝑏−1,𝑦𝑏+1). The new chip coordinates (𝑥′,𝑦′) must satisfy the conditions 1≤𝑥′≤ℎ and 1≤𝑦′≤𝑤.
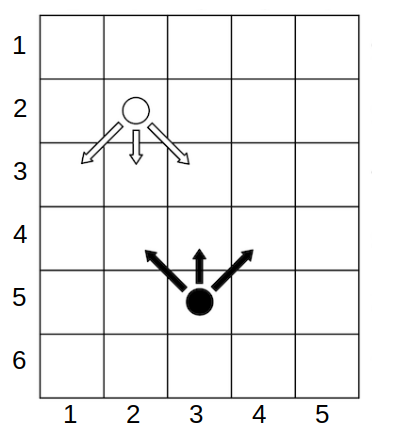
Example game state. Alice plays with the white chip, Bob with the black one. Arrows indicate possible moves.
A player immediately wins if they place their chip in a cell occupied by the other player's chip. If either player cannot make a move (Alice—if she is in the last row, i.e. 𝑥𝑎=ℎ, Bob—if he is in the first row, i.e. 𝑥𝑏=1), the game immediately ends in a draw.
What will be the outcome of the game if both opponents play optimally?
Input
Each test consists of multiple test cases. The first line contains a single integer 𝑡 (1≤𝑡≤10^4) — the number of test cases. This is followed by the description of the test cases.
Each test case consists of a single line containing six integers ℎ, 𝑤, 𝑥𝑎, 𝑦𝑎, 𝑥𝑏, 𝑦𝑏 (1≤𝑥𝑎,𝑥𝑏≤ℎ≤10^6, 1≤𝑦𝑎,𝑦𝑏≤𝑤≤10^9) — the dimensions of the board and the initial positions of Alice's and Bob's chips. It is guaranteed that either 𝑥𝑎≠𝑥𝑏 or 𝑦𝑎≠𝑦𝑏.
It is guaranteed that the sum of ℎ over all test cases does not exceed 10^6.
Output
For each test case, output "Alice" if Alice wins, "Bob" if Bob wins, and "Draw" if neither player can secure a victory. You can output each letter in any case (lowercase or uppercase). For example, the strings "bOb", "bob", "Bob", and "BOB" will be accepted as Bob's victory.
Example
input
12
6 5 2 2 5 3
4 1 2 1 4 1
1 4 1 3 1 1
5 5 1 4 5 2
4 4 1 1 4 4
10 10 1 6 10 8
10 10 2 6 10 7
10 10 9 1 8 1
10 10 8 1 10 2
10 10 1 1 2 1
10 10 1 3 4 1
10 10 3 1 1 1
output
Alice
Bob
Draw
Draw
Draw
Alice
Draw
Draw
Bob
Alice
Alice
Draw회고
대회에서는 피하고 싶던 시뮬레이션 문제였다.
하지만 다른 문제들이 마땅히 떠오르지 않아 마지막까지 붙들고 있다가 풀지 못했다.
대회가 끝나고 다음날 풀어보니 정면에 있을 때 (y1 == y2) 이기는 상대가 직진하지 않고 왼쪽 아니면 오른쪽으로 이동시켜 버린 것이 예외를 만들어버렸다.
풀이
What will be the outcome of the game if both opponents play optimally?
두 상대 플레이어가 최적으로 (optimally) 플레이한다면 결과는?
이 글귀에서 optimally (최적의) 라는 단어가 핵심이였다.
먼저 두 플레이어의 칩의 세로거리가 홀수라면 앨리스가 이기고 (앨리스가 선 플레이어이므로), 짝수라면 밥이 이긴다는 것을 떠올렸다.
그러면 아래의 세가지에 유의하며 풀 수 있다.
- 이기는 플레이어는 적이 있는 방향으로 이동할 것
- 지는 플레이어는 적이 있는 반대방향으로 이동할 것 (절대 이길 수 없으므로 Draw 만드려고 한다.)
- 같은 줄에 있다면 (y1 == y2) 누군가가 이긴 것 (Draw 가 될 수 없는 상황)
누가 이기는지 (alice_win) 와 누가 왼쪽에 있는지 (alice_left), 그리고 누구의 턴인지 (alice_turn) 를 확인하는 변수를 우선 만들었다.
그 후 for 문을 x2,x1 거리만큼 돌도록 만들었다.
그리고 각 플레이어의 턴 마다 위 세가지에 유의하며 행동하도록 작성.
끝.
def move(y, direction):
if direction == 'L':
if y > 1: # 제일 왼쪽 좌표
return -1
else:
if y < w: # 제일 오른쪽 좌표
return 1
return 0
t = int(input())
for _ in range(t):
h, w, x1, y1, x2, y2 = map(int, input().split())
alice_win = (x2 - x1) % 2 == 1
alice_left = y2 - y1 > 0
alice_turn = True
for i in range(x2 - x1):
if alice_turn:
x1 += 1
if (alice_win and alice_left) or (not alice_win and not alice_left): # 앨리스가 이기고 밥이 오른쪽에 있거나, 앨리스가 지고 앨리스가 오른쪽에 있을 때
y1 += move(y1,'R') # 오른쪽으로 이동
elif alice_win and y1 == y2:
pass
else:
y1 += move(y1,'L')
else:
x2 -= 1
if (alice_win and alice_left) or (not alice_win and not alice_left):
y2 += move(y2,'R')
else:
y2 += move(y2,'L')
alice_turn = not alice_turn
if y1 == y2: # 상대를 잡았을 때
if alice_win:
print('Alice')
else:
print('Bob')
break
else:
print('Draw')